It is important to distinguish between the knowledge in the mind of an agent and the knowledge in the mind of the designer of the agent. Consider the extreme cases:

• •

  At one extreme is a highly specialized agent that works well in the environment for which it was designed, but is helpless outside of this niche. The designer may have done considerable work in building the agent, but the agent can be extremely specialized to operate well. An example is a traditional thermostat. It may be difficult to design a thermostat so that it turns on and off at exactly the right temperatures, but the thermostat itself does not have to do much computation. Another example is a car-painting robot that always paints the same parts in an automobile factory. There may be much design time or offline computation to get it to work perfectly, but the painting robot can paint parts with little online computation; it senses that there is a part in position, but then it carries out its predefined actions. These very specialized agents do not adapt well to different environments or to changing goals. The painting robot would not notice if a different sort of part were present and, even if it did, it would not know what to do with it. It would have to be redesigned or reprogrammed to paint different parts or to change into a sanding machine or a dog-washing machine.

• •

  At the other extreme is a very flexible agent that can survive in arbitrary environments and accept new tasks at run time. Simple biological agents such as insects can adapt to complex changing environments, but they cannot carry out arbitrary tasks. Designing an agent that can adapt to complex environments and changing goals is a major challenge. The agent will know much more about the particulars of a situation than the designer. Even biology has not produced many such agents. Humans may be the only extant example, but even humans need time to adapt to new environments.

Even if the flexible agent is our ultimate dream, researchers have to reach this goal via more mundane goals. Rather than building a universal agent, which can adapt to any environment and solve any task, researchers have been restricted to particular agents for particular environmental niches. The designer can exploit the structure of the particular niche and the agent does not have to reason about other possibilities.

Two broad strategies have been pursued in building agents:

• •

  The first is to simplify environments and build complex reasoning systems for these simple environments. For example, factory robots can do sophisticated tasks in the engineered environment of a factory, but they may be hopeless in a natural environment. Much of the complexity of the task can be reduced by simplifying the environment. This is also important for building practical systems because many environments can be engineered to make them simpler for agents.

• •

  The second strategy is to build simple agents in natural environments. This is inspired by seeing how insects can survive in complex environments even though they have very limited reasoning abilities. Modern language systems can predict the probability of the next word in an arbitrary text, but this does not mean they can be used for decision making. Researchers then make the agents have more reasoning abilities as their tasks become more complicated.

One of the advantages of simplifying environments is that it may enable us to prove properties of agents or to optimize agents for particular situations. Proving properties or optimization typically requires a model of the agent and its environment. The agent may do a little or a lot of reasoning, but an observer or designer of the agent may be able to reason about the agent and the environment. For example, the designer may be able to prove whether the agent can achieve a goal, whether it can avoid getting into situations that may be bad for the agent (safety), whether it can avoid getting stuck somewhere (liveness), or whether it will eventually get around to each of the things it should do (fairness). Of course, the proof is only as good as the model.

The advantage of building agents for complex environments is that these are the types of environments in which humans live and where agents could be useful.

Even natural environments can be abstracted into simpler environments. For example, for an autonomous car driving on public roads the environment can be conceptually simplified so that everything is either a road, another car, or something to be avoided. Although autonomous cars have sophisticated sensors, they only have limited actions available, namely steering, accelerating, and braking.

Fortunately, research along both lines, and between these extremes, is being carried out. In the first case, researchers start with simple environments and make the environments more complex. In the second case, researchers increase the complexity of the behaviors that the agents can carry out.

One way that AI representations differ from computer programs in traditional languages is that an AI representation typically specifies what needs to be computed, not how it is to be computed. You might specify that the agent should find the most likely disease a patient has, or specify that a robot should get coffee, but not give detailed instructions on how to do these things. Much AI reasoning involves searching through the space of possibilities to determine how to complete a task.

Typically, a task is only given informally, such as “deliver parcels promptly when they arrive” or “fix whatever is wrong with the electrical system of the home.”

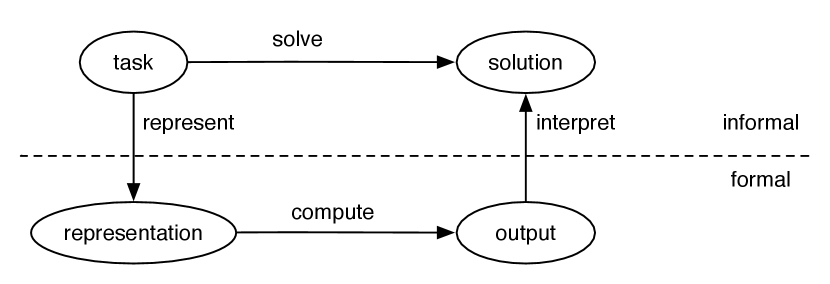
The general framework for solving tasks by computer is given in Figure 1.9. To solve a task, the designer of a system must:

• •

  determine what constitutes a solution

• •

  represent the task in a way a computer can reason about

• •

  use the computer to compute an output; either answers presented to a user or actions to be carried out in the environment

• •

  interpret the output as a solution to the task.

In AI, knowledge is long-term representation of a domain whereas belief is about the immediate environment, for example where the agent is and where other object are. In philosophy, knowledge is usually defined as justified true belief, but in AI the term is used more generally to be any relatively stable information, as opposed to belief, which is more transitory information. The reason for this terminology is that it is difficult for an agent to determine truth, and “justified” is subjective. Knowledge in AI can be represented in terms of logic, neural networks, or probabilistic models, but belief is typically represented as a distribution over the states.

A representation of some piece of knowledge is the particular data structures used to encode the knowledge so it can be reasoned with.

The form of representation – what is represented – is a compromise among many competing objectives. A representation should be:

• •

  rich enough to express the knowledge needed to solve the task

• •

  as close to a natural specification of the task as possible

• •

  amenable to efficient computation

• •

  able to be acquired from people, data, and past experiences.

Being as close to a natural specification of the task as possible means should be compact, natural, and maintainable. It should be easy to see the relationship between the representation and the domain being represented, so that it is easy to determine whether the knowledge represented is correct; a small change in the task should result in a small change in the representation of the task. There is an active debate about how much of the internal structure of reasoning should be explainable; the field of explainable AI is about how to make more aspects of the decision making amenable to being explained to a person.

Efficient computation enables the agent to act quickly enough to be effective. A tractable algorithm is one with reasonable asymptotic complexity, often meaning the computation time is polynomial in the input size, however often linear complexity is too slow. To ensure this, representations exploit features of the task for computational gain and trade off accuracy and computation time.

Many different representation languages have been designed. Many of these start with some of these objectives and are then expanded to include the other objectives. For example, some are designed for learning, perhaps inspired by neurons, and then expanded to allow richer task-solving and inference abilities. Some representation languages are designed with expressiveness in mind, and then inference and learning are added on. Some language designers focus on tractability and enhance richness, naturalness, and the ability to be acquired.

Given an informal description of a task, before even considering a computer, an agent designer should determine what would constitute a solution. This question arises not only in AI but in any software design. Much of software engineering involves refining the specification of the task.

Tasks are typically not well specified. Not only is there usually much left unspecified, but also the unspecified parts cannot be filled in arbitrarily. For example, if a user asks a trading agent to find out all the information about resorts that may have unsanitary food practices, they do not want the agent to return all the information about all resorts, even though all of the information requested is in the result. However, if the trading agent does not have complete knowledge about the resorts, returning all of the information may be the only way for it to guarantee that all of the requested information is there. Similarly, one does not want a delivery robot, when asked to take all of the trash to the garbage can, to take everything to the garbage can, even though this may be the only way to guarantee that all of the trash has been taken. Much work in AI is motivated by commonsense reasoning; the computer should be able to reach commonsense conclusions about the unstated assumptions.

Given a well-defined task, the next issue is whether it matters if the answer returned is incorrect or incomplete. For example, if the specification asks for all instances, does it matter if some are missing? Does it matter if there are some extra instances? Often a person does not want just any solution but the best solution according to some criteria. There are four common classes of solutions:

Optimal solution

An optimal solution to a task is one that is the best solution according to some measure of solution quality. This measure is typically specified as an ordinal, where only the order matters. In some situations a cardinal measure, where the relative magnitudes also matter, is used. For example, a robot may need to take out as much trash as possible; the more trash it can take out, the better. In a more complex example, you may want the delivery robot to take as much of the trash as possible to the garbage can, minimizing the distance traveled, and explicitly specify a trade-off between the effort required and the proportion of the trash taken out. There are also costs associated with making mistakes and throwing out items that are not trash. It may be better to miss some trash than to waste too much time. One general measure of desirability that interacts with probability is utility.

Satisficing solution

Often an agent does not need the best solution to a task but just needs some solution. A satisficing solution is one that is good enough according to some description of which solutions are adequate. For example, a person may tell a robot that it must take all of the trash out, or tell it to take out three items of trash.

Approximately optimal solution

One of the advantages of a cardinal measure of success is that it allows for approximations. An approximately optimal solution is one whose measure of quality is close to the best that could theoretically be obtained. Typically, agents do not need optimal solutions to tasks; they only need to get close enough. For example, the robot may not need to travel the optimal distance to take out the trash but may only need to be within, say, $10\%$ of the optimal distance. Some approximation algorithms guarantee that a solution is within some range of optimal, but for some algorithms no guarantees are available.

For some tasks, it is much easier computationally to get an approximately optimal solution than to get an optimal solution. However, for other tasks, it is just as difficult to find an approximately optimal solution that is guaranteed to be within some bounds of optimal as it is to find an optimal solution.

Probable solution

A probable solution is one that, even though it may not actually be a solution to the task, is likely to be a solution. This is one way to approximate, in a precise manner, a satisficing solution. For example, in the case where the delivery robot could drop the trash or fail to pick it up when it attempts to, you may need the robot to be 80% sure that it has picked up three items of trash. Often you want to distinguish a false-positive error (positive answers that are not correct) from a false-negative error (negative answers that are correct). Some applications are much more tolerant of one of these types of errors than the other.

These categories are not exclusive. A form of learning known as probably approximately correct (PAC) learning considers probably learning an approximately correct concept.

Once you have some requirements on the nature of a solution, you must represent the task so a computer can solve it.

Computers and human minds are examples of physical symbol systems. A symbol is a meaningful pattern that can be manipulated. Examples of symbols are written words, sentences, gestures, marks on paper, or sequences of bits. A symbol system creates, copies, modifies, and destroys symbols. Essentially, a symbol is one of the patterns manipulated as a unit by a symbol system. The term “physical” is used, because symbols in a physical symbol system are physical objects that are part of the real world, even though they may be internal to computers and brains. They may also need to physically affect action or motor control.

The physical symbol system hypothesis of Newell and Simon [1976] is that:

A physical symbol system has the necessary and sufficient means for general intelligent action.

This is a strong hypothesis. It means that any intelligent agent is necessarily a physical symbol system. It also means that a physical symbol system is all that is needed for intelligent action; there is no magic or as-yet-to-be-discovered quantum phenomenon required. It does not imply that a physical symbol system does not need a body to sense and act in the world.

One aspect of this hypothesis is particularly controversial, namely whether symbols are needed at all levels. For example, consider recognizing a “cat” in a picture. At the top level is the symbol for a cat. At the bottom level are pixels from a camera. There are many intermediate levels that, for example, combine pixels to form lines and textures. These intermediate features are learned from data, and are not learned with the constraint that they are interpretable. Although some people have tried to interpret them, it is reasonable to say that these are not symbols. However, at a high level, they are either trained to be symbols (e.g., by learning a mapping between pixels and symbols, such as cat) or can be interpreted as symbols.

An agent can use a physical symbol system to model the world. A model of a world is a representation of an agent’s beliefs about what is true in the world or how the world changes. The world does not have to be modeled at the most detailed level to be useful. All models are abstractions; they represent only part of the world and leave out many of the details. An agent can have a very simplistic model of the world, or it can have a very detailed model of the world. The level of abstraction provides a partial ordering of abstraction. A lower-level abstraction includes more details than a higher-level abstraction. An agent can have multiple, even contradictory, models of the world. Models are judged not by whether they are correct, but by whether they are useful.

Choosing an appropriate level of abstraction is difficult for the following reasons:

• •

  A high-level description is easier for a human to specify and understand.

• •

  A low-level description can be more accurate and more predictive. Often, high-level descriptions abstract away details that may be important for actually solving the task.

• •

  The lower the level, the more difficult it is to reason with. This is because a solution at a lower level of detail involves more steps and many more possible courses of action exist from which to choose.

• •

  An agent may not know the information needed for a low-level description. For example, the delivery robot may not know what obstacles it will encounter or how slippery the floor will be at the time that it must decide what to do.

It is often a good idea to model an environment at multiple levels of abstraction. This issue is discussed further in Section 2.2.

Biological systems, and computers, can be described at multiple levels of abstraction. At successively lower levels of animals are the neuronal level, the biochemical level (what chemicals and what electrical potentials are being transmitted), the chemical level (what chemical reactions are being carried out), and the level of physics (in terms of forces on atoms and quantum phenomena). What levels above the neuronal level are needed to account for intelligence is still an open question. These levels of description are echoed in the hierarchical structure of science itself, where scientists are divided into physicists, chemists, biologists, psychologists, anthropologists, and so on. Although no level of description is more important than any other, it is plausible that you do not have to emulate every level of a human to build an AI agent but rather you can emulate the higher levels and build them on the foundation of modern computers. This conjecture is part of what AI studies.

The following are two levels that seem to be common to both biological and computational entities:

• •

  The knowledge level is the level of abstraction that considers what an agent knows and believes and what its goals are. The knowledge level considers what an agent knows, but not how it reasons. For example, the delivery agent’s behavior can be described in terms of whether it knows that a parcel has arrived or not and whether it knows where a particular person is or not. Both human and robotic agents are describable at the knowledge level. At this level, you do not specify how the solution will be computed or even which of the many possible strategies available to the agent will be used.

• •

  The symbol level is a level of description of an agent in terms of the reasoning it does. To implement the knowledge level, an agent manipulates symbols to produce answers. Many cognitive science experiments are designed to determine what symbol manipulation occurs during reasoning. Whereas the knowledge level is about what the agent believes about the external world and what its goals are in terms of the outside world, the symbol level is about what goes on inside an agent to reason about the external world.