16 Knowledge Graphs and Ontologies 16.1 Knowledge Graphs 16.3 Ontologies and Knowledge Sharing

16.2 Classes and Properties

Typically, you know more about a domain than a database of facts; you may know general rules from which other facts can be derived. Which facts are explicitly given and which are derived is a choice to be made when designing and building a knowledge base.

Primitive knowledge is knowledge that is specified explicitly. Derived knowledge is knowledge that can be inferred from primitive knowledge and other derived knowledge.

The use of rules allows for a more compact representation of knowledge. Derived relations allow for generalizations to be drawn from knowing something is in a class. This is important because you do not directly observe everything about a domain. Much of what is known about a domain is inferred from the observations and more general knowledge, including learned knowledge.

A standard way to use derived knowledge is to specify attributes (property–value pairs) that hold for all members of a class. Individuals inherit the attributes associated with the classes they are in. Grouping individuals into classes enables a more concise representation than representing the attributes for each individual separately. This issue was discussed in the context of probabilistic classifiers and unsupervised learning.

A class is the set of those actual and potential individuals that would be members of the class. This is typically an intensional set, defined by a characteristic function that is true of members of the set and false of other individuals. The alternative to an intensional set is an extensional set, which is defined by listing its elements.

For example, the class $c h a i r$ is the set of all things that would be chairs. The definition is not the set of things that are chairs, because chairs that have not yet been built also fall into the class of chairs. Without this definition, an agent could not design a chair, because the chair doesn’t exist during the designing (and may never exist).

Two classes are not equivalent just because they have the same members. For example, the class of green unicorns and the class of chairs that are exactly 124 meters high are different classes, even though they may contain the same elements; they are both empty. A green unicorn is not a 124 meter high chair.

The definition of class allows any set that can be described to be a class. For example, the set consisting of the number 17, the Taj Mahal in Agra, and the first goal scored in the 2022 FIFA world cup final can be considered a class, but it is not very useful. A natural kind is a class such that describing individuals using the class is more succinct than describing individuals without the class. For example, “mammal” is a natural kind, because describing the common attributes of mammals makes a knowledge base that uses “mammal” more succinct than one that does not use “mammal” and instead repeats the attributes for every individual.

16.2.1 Class and Property Hierarchies

Class $S$ is a subclass of class $C$ means $S$ is a subset of $C$ . That is, every individual of type $S$ is of type $C$ .

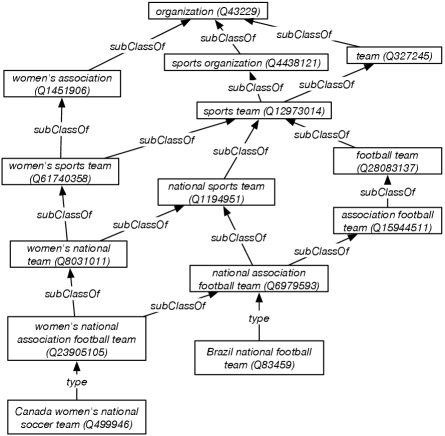
Refer to caption — Figure 16.2: Part of the Wikidata class structure for the Brazil national football team and the Canada women’s national soccer team

Example 16.8.

Figure 16.2 shows the class structure for the Brazil national football team and the Canada women’s national soccer team, up to the level of organization. Shown is the English name of the entity or class with the Wikidata identifier in parentheses.

At the lowest level, the Brazil national football team is an instance of the class Q6979593, which has the name in English “national association football team”. This is a subclass of the classes called “national football team” and “association football team”.

The relationship between types and subclasses can be written as a definite clause:

{prop}(E,type,C)\leftarrow\mbox{}

{prop}(S,subClassOf,C)\wedge\mbox{}\mbox{}

{prop}(E,type,S).

or using functional notation, if $subClassOf(S,C)$ and $type(E,S)$ , then $type(E,C)$ .

You can treat $t y p e$ and $s u b C l a s s O f$ as special properties that allow property inheritance. Property inheritance occurs when a value for a property is specified at the class level and inherited by the members of the class. If all members of class $c$ have value $v$ for property $p$ , this can be written as the definite clause

{prop}(Ind,p,v)\leftarrow\mbox{}

{prop}(Ind,type,c).

which, together with the above rule that relates types and subclasses, can be used for property inheritance.

Property $p_{1}$ is a sub-property of property $p_{2}$ if every pair related by $p_{1}$ is also related by $p_{2}$ . In functional notation this means $p_{1}(x,y)$ implies $p_{2}(x,y)$ , or in triple notation $(x,p_{1},y)$ implies $(x,p_{2},y)$ .

Example 16.9.

Some sub-properties in Wikidata are

•

“member of sports team” (P54) is a sub-property of “member of” (P463)
•

“member of” (P463) is a sub-property of “affiliation” (P1416)
•

“affiliation” (P1416) is a sub-property of “part of” (P361)
•

“part of” (P361) is a sub-property of “partially coincident with” (P1382)
•

“partially coincident with” (P1382) is a sub-property of “different from” (P1889).

The domain of a property is a class such that the subject (first argument) of a triple with the property has to be in the class. That is, “the domain of property $p$ is class $C$ ” means if $p(x,y)$ then $x\in C$ . If a property $p$ has domain $C_{1}$ and has domain $C_{2}$ , then every individual in the subject of $p$ must be in both $C_{1}$ and $C_{2}$ .

The range of a property is a class such that the object (last argument) of a triple with the property has to be in the class. That is, the range of property $p$ is class $C$ means if $p(x,y)$ then $y\in C$ .

A property $p$ is functional means that there is at most one object associated with any subject; i.e., if $p(x,y_{1})$ and $p(x,y_{2})$ then $y_{1}=y_{2}$ . This corresponds to the mathematical definition of a partial function.

Functional properties play a special role in relational learning and relational probabilistic models in Chapter 17, because features, as used in constraint satisfaction problems and in machine learning, and random variables are assumed to be functional (having only one value). What is special here is that non-functional properties such as “has-friend” are allowed.

Example 16.10.

The following are not (currently) part of Wikidata, but could be:

•

the domain of “member of sports team” (P54) is “human” (Q5)
•

the range of “member of sports team” (P54) is “sports team” (Q12973014)
•

“member of sports team” (P54) is not functional, because someone could be in multiple sports teams at the same time; as shown in Figure 16.1, Christine Sinclair was in two sports teams
•

“date of birth” (P569) is functional as each person has only one date of birth.

Some general guidelines are useful for deciding what should be primitive and what should be derived:

•

When associating an attribute with an individual, select the most general class $C$ that the individual is in, where all members of $C$ have that attribute, and associate the attribute with class $C$ . Inheritance can be used to derive the attribute for the individual and all other members of class $C$ . This representation methodology tends to make knowledge bases more concise, and it means that it is easier to incorporate new individuals because members of $C$ automatically inherit the attribute. For example, people have backbones; this is represented by having a class of vertebrates which humans are a subclass of.
•

Do not associate a contingent attribute of a class with the class. A contingent attribute is one whose value changes when circumstances change. For example, do not define a football team in terms of having a coach; a team does not stop being a team because the coach resigns or dies.

Classes in Knowledge Bases and Object-Oriented Programming

The use of “individuals” and “classes” in knowledge-based systems is very similar to the use of “objects” and “classes” in object-oriented programming (OOP) languages such as Smalltalk, Python, or Java. This should not be too surprising because they have an interrelated history. But there are important differences that tend to make the direct analogy often more confusing than helpful:

•

Objects in OOP are computational objects; they are data structures and associated programs. A “person” object in Java is not a person. However, individuals in a knowledge base (KB) are (typically) things in the real world. A “person” individual in a KB can be a real person. A “chair” individual can be a real chair you can actually sit in; it can hurt you if you bump into it. You can send a message to, and get answers from, a “chair” object in Java, whereas a chair in the real world tends to ignore what you tell it. A KB is not typically used to interact with a chair, but to reason about a chair. A real chair stays where it is unless it is moved by a physical agent.
•

In a KB, a representation of an object is only an approximation at one (or a few) levels of abstraction. Real objects tend to be much more complicated than what is represented. You typically do not represent the individual fibers in the fabric of a chair. In an OOP system, there are only the represented properties of an object. The system can know everything about a Java object, but not about a real individual.
•

The class structure of Java is intended to represent designed objects. A systems analyst or a programmer gets to create a design. For example, in Java, an object is only a member of one lowest-level class. There is no multiple inheritance. Real objects are not so rigidly constrained. The same person could be a football coach, a mathematician, and a mother.
•

A computer program cannot be uncertain about its data structures; it has to select particular data structures to use. However, you can be uncertain about the types of things in the world.
•

The representations in a KB do not actually do anything. In an OOP system, objects do computational work. In a KB, they just represent – that is, they just refer to objects in the world.
•

While an object-oriented modeling language, like UML, may be used for representing KBs, it may not be the best choice. A good OO modeling tool has facilities to help build good designs. However, the world being modeled may not have a good design at all. Trying to force a good design paradigm on a messy world may not be productive.

Knublauch et al. [2006] present a more detailed comparison between object-orientated software design and the use of ontologies.

16.2.2 Designing Classes

Categorizing objects, the basis for modern ontologies, has a long history. Aristotle [350 BCE] suggested the definition of a class $C$ in terms of

•

Genus: a superclass of $C$ . The plural of genus is genera.
•

Differentia: the attributes that make members of the class $C$ different from other members of the superclass of $C$ .

He anticipated many of the issues that arise in definitions:

If genera are different and co-ordinate, their differentiae are themselves different in kind. Take as an instance the genus “animal” and the genus “knowledge”. “With feet”, “two-footed”, “winged”, “aquatic”, are differentiae of “animal”; the species of knowledge are not distinguished by the same differentiae. One species of knowledge does not differ from another in being “two-footed”.

– Aristotle [350 BCE]

Note that “co-ordinate” here means neither is subordinate to the other.

In the style of modern ontologies, we would say that “animal” is a class and “knowledge” is a class. The property “two-footed” has domain “animal”. If something is an instance of knowledge, it does not have a value for the property “two-footed”.

The art of ranking things in genera and species is quite important, and greatly helps our judgment as well as our memory. …This helps one not merely to retain things in one’s memory, but also to find them there. Writers who have laid out all sorts of notions under certain headings or categories have done something very useful.

– Leibniz [1705]

To build an ontology based on Aristotelian definitions:

•

For each class you may want to define, determine a relevant superclass and then select those attributes that distinguish the class from other subclasses. Each attribute gives a property and a value.
•

For each property, define the most general class for which it makes sense, and define the domain of the property to be this class. Make the range of the property another class that makes sense (perhaps requiring this range class to be defined, either by enumerating its values or by defining it using an Aristotelian definition).

Example 16.11.

In Example 16.8, a national sports team is a “team that represents a nation in a sport”, where “team” is the genus and “represents a nation in a sport” is the differentia. An association football team is a sports team that plays association football (soccer). So a national association football team is a team that represents a nation in association football, and so is a subclass of both. A team is “a group linked in a common purpose”.

In Figure 16.2, the differentia that distinguishes the classes on the left is that the members have to be women. There can also be a women’s association football team, a women’s football team, and a women’s team, not all of which are given identifiers in Wikidata. Note that, while “men’s football team” defines a class, it does not exist in Wikidata because most teams allow women, even if none actually play.

The class hierarchy is a directed graph with arcs from subclasses to their immediate superclasses. Cyclic definitions are not useful; for example, defining $x$ is above $y$ as $y$ is below $x$ and defining $y$ is below $x$ as $x$ is above $y$ does not define either; it just creates an equivalence. Thus, it is reasonable to assume that the graph is a directed acyclic graph (DAG), forming a lattice. This methodology does not, in general, give a tree hierarchy of classes. Objects can be in many classes. Each class does not have a single most-specific superclass.

Example 16.12.

Consider the definitions of rectangle, rhombus, and square:

•

A rectangle is a quadrilateral where all inside angles are right angles ( $90\degree$ ).
•

A rhombus is a quadrilateral where all four sides have the same length.
•

A square is a quadrilateral where all four sides have the same length and all inside angles are right angles.

A square is both a rectangle and a rhombus; both are most specific superclasses. A square could be defined as a rectangle where all sides have the same length. It could equally well be defined as a rhombus where the inside angles are right angles.

A quadrilateral is a planar figure made up of four straight sides. The definition of square can be expanded so that a square is a planar figure made up of four straight sides of equal length and the inside angles are right angles.

In rare cases, the natural class hierarchy forms a tree, most famously in the Linnaean taxonomy of living things. The reason this is a tree is because of evolution. Trying to force a tree structure in other domains has been much less successful.

If the class structure is acyclic and each class – except for a top class, which we call thing – is defined in terms of a superclass and the attributes that form the differentia, then each class has a normal form as thing conjoined with attributes, by replacing each superclass by its definition. If the attributes are property–value pairs then one class is a subclass of the other if its normal form is a superset of the other; Section 16.3.1 describes more expressive class constructs. In Example 16.12, square is a subclass of rectangle and is a subclass of rhombus as all of the attributes are the same, with an extra one for the differentia of the square.

Artificial Intelligence 3E